DeepSpeed with 1-bit Adam: 5x less communication and 3.4x faster training

1. Introduction

Scalable training of large models (like BERT and GPT-3) requires careful optimization rooted in model design, architecture, and system capabilities. From a system standpoint, communication has become a major bottleneck, especially on commodity systems with standard TCP interconnects that offer limited network bandwidth. Communication compression is an important technique to reduce training time on such systems. One of the most effective ways to compress communication is via error compensation compression, which offers robust convergence speed, even under 1-bit compression. However, state-of-the-art error compensation techniques only work with basic optimizers like Stochastic Gradient Descent (SGD) and momentum SGD, which are linearly dependent on the gradients. They do not work with non-linear gradient-based optimizers like Adam, which offers state-of-the-art convergence efficiency and accuracy for many tasks, including training of BERT-like models. For a powerful optimizer like ADAM, the non-linear dependency on gradient (in the variance term) makes it challenging to develop error compensation-based compression techniques, limiting the practical value of the state-of-the-art communication compression techniques.

1.1 Background: Classic compression techniques

One way of communication compression is 1-bit compression, which can be expressed as:

With this compression, we could achieve a 32x reduction of memory size by representing each number using one bit. The problem is that using this straightforward method would significantly degrade the convergence speed, which makes this method inapplicable. To solve this problem, recent studies show that by using error compensation compression, we could expect almost the same convergence rate with communication compression. The idea of error compensation can be summarized as: 1) doing compression, 2) memorizing the compression error, and then 3) adding the compression error back in during the next iteration. For SGD, doing error compression leads to:

Where C(⋅) is the 1-bit compression operator. The good thing about doing this error compensation is that the history compression error (e_t and e_(t-1)) would be canceled by itself eventually, which can be seen by:

This strategy has been proven to work for optimization algorithms that are linearly dependent on the gradient, such as SGD and Momentum SGD.

1.2 Challenges in applying error-compensation to Adam

We provide an overview of the Adam algorithm below. The update rules are as follows.

As shown in the equations above, the variance term v_t is nonlinearly dependent on the gradient g_t. If we apply basic error compensation compression to Adam, we observe that Adam will not converge as shown in Figure 1.

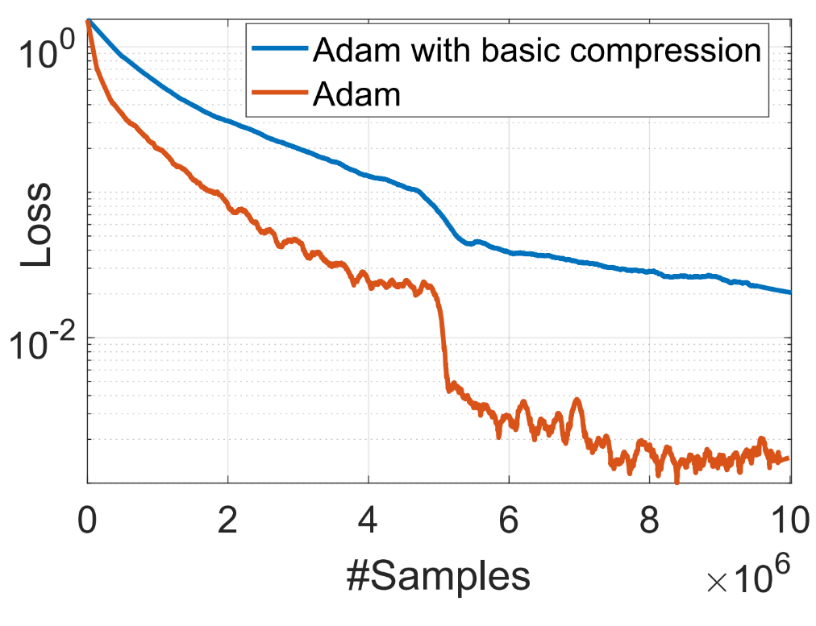
Figure 1: Inapplicability of Error-compensation Compression for Adam due to non-linear dependence on the gradient

2. Compressing communication with 1-bit Adam

To compress communication while using the Adam optimizer, we develop 1-bit Adam, which addresses the non-linearity in gradients via preconditioning. We observe that the magnitude of changes on the non-linear term, variance ( v_t), decrease significantly after a few epochs of training and setting v_t constant afterwards will not change the convergence speed. The proposed 1-bit Adam optimizer, as shown in Figure 2, consists of two parts: the warmup stage, which is essentially the vanilla Adam algorithm; and the compression stage, which keeps the variance term constant and compresses the remaining linear term, that is the momentum, into 1-bit representation.

The compression stage of the algorithm is controlled by a threshold parameter (as shown in Figure 2). When we detect that the change in “variance” falls below a certain threshold, we switch to the compression stage. Our study shows that only 15-20% of the overall training steps are needed for the warmup stage.

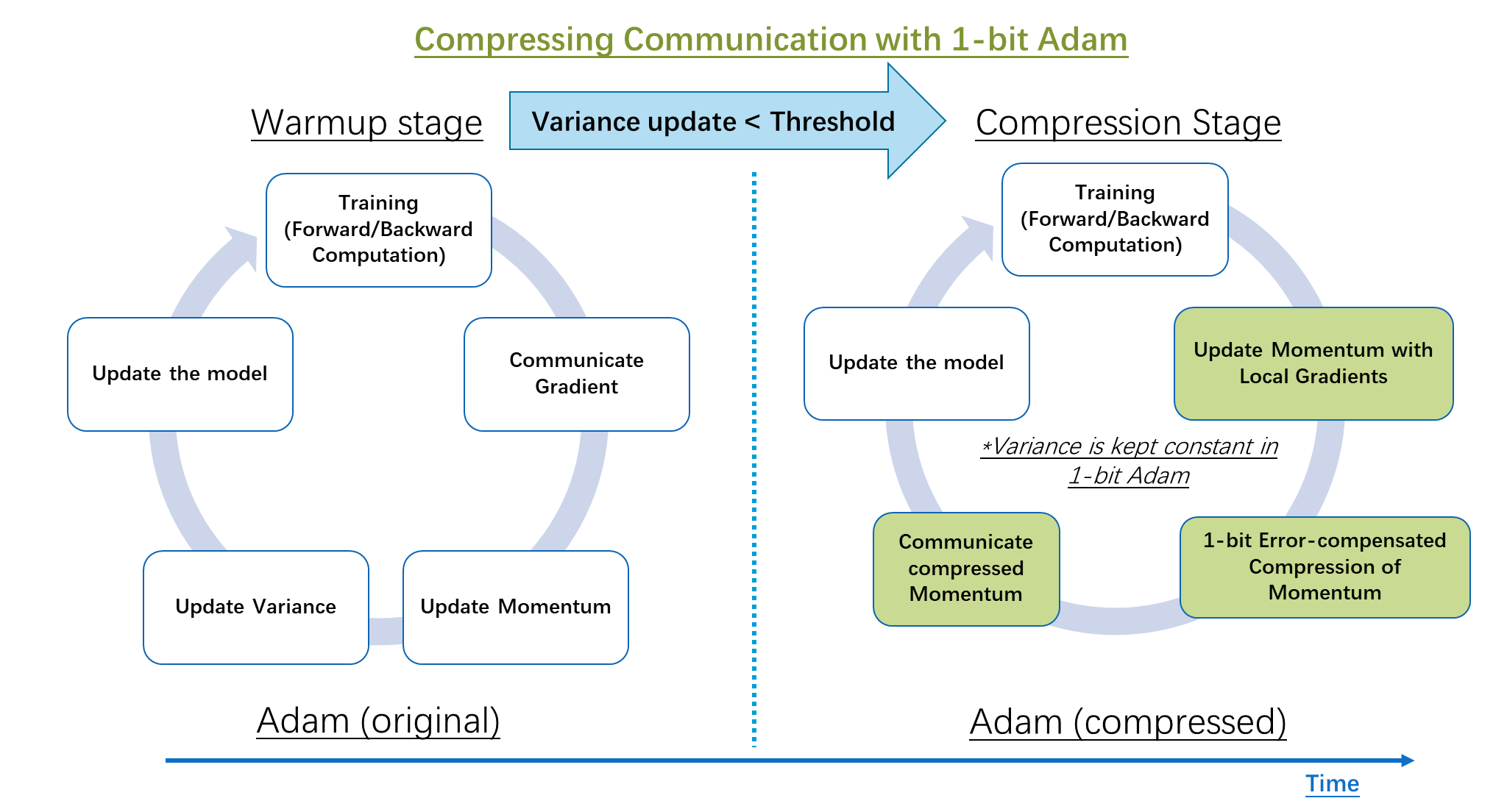
Figure 2: Comparison of distributed training steps in classic Adam and the proposed 1-bit compressed Adam algorithm

2.1 How 1-bit Adam works under the hood

The weight update rule for 1-bit Adam is governed by the following equations.

For the i-th worker, in the compression stage:

Where x_t is the model after iteration (t-1), m_t^(i), e_t^(i) are the momentum and compression error on worker i after iteration (t-1), and v_warmup is the variance term after the warmup stage.

2.2 Addressing system challenges for 1-bit Adam

Besides the algorithmic challenge, there are two system challenges in applying 1-bit Adam in training systems. First, we need efficient kernels that convert the momentum to 1-bit representations. Second, we need efficient communication schemes to exchange this compressed momentum across different GPUs. The goal of compression is to reduce the overall training time so that commodity systems with bandwidth-limited interconnects can be used to train large models. We address these challenges in DeepSpeed and introduce a fully optimized 1-bit Adam implementation for training on communication-constrained systems.

3. Benefits of 1-bit Adam on communication-constrained systems

1-bit Adam offers the same convergence as Adam, incurs up to 5x less communication that enables up to 3.5x higher throughput for BERT-Large pretraining and up to 2.7x higher throughput for SQuAD fine-tuning. This end-to-end throughput improvement is enabled by the 6.6x (Figure 3) and 6.2x (Figure 4) speedup observed during the compression stage. It is worth mentioning that our 1-bit Adam optimizer scales so well on a 40 Gigabit Ethernet system that its performance is comparable to Adam’s scalability on a 40 Gigabit InfiniBand QDR system. We note that the effective bandwidth on 40 Gigabit Ethernet is 4.1 Gbps based on iperf benchmarks whereas InfiniBand provides near-peak bandwidth of 32Gbps based on InfiniBand perftest microbenchmarks.

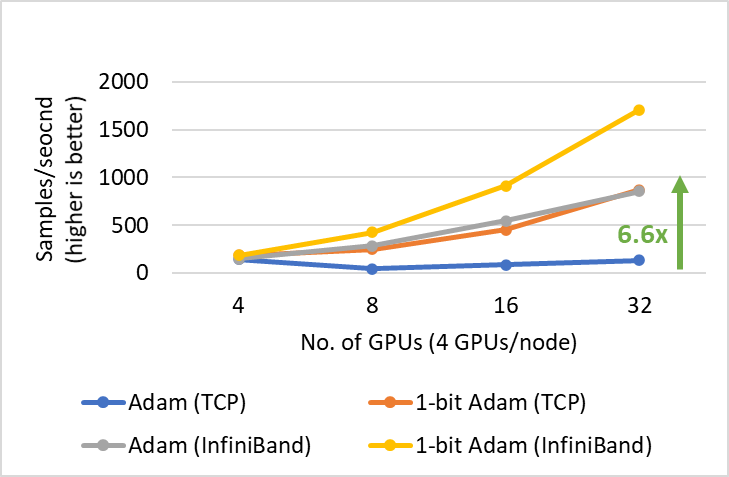
Figure 3: Scalability of 1-bit Adam for BERT-Large Pretraining on V100 GPUs with batch size of 16/GPU.

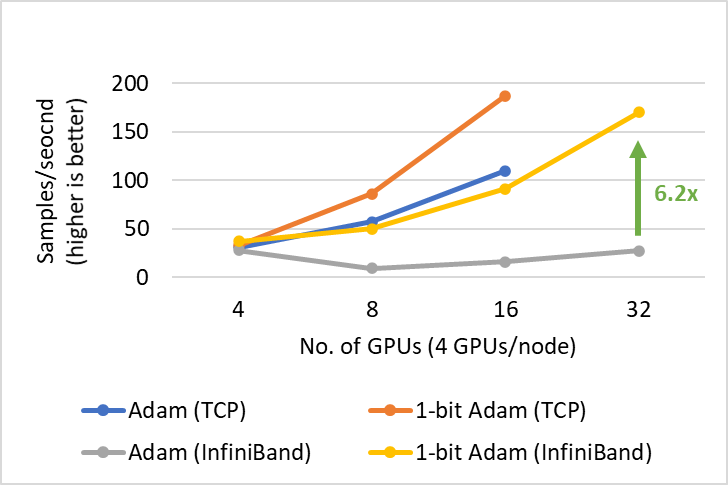
Figure 4: Scalability of 1-bit Adam for SQuAD Finetuning on V100 GPUs with batch size of 3/GPU.

4. Dive deeper into 1-bit Adam evaluation results

Same convergence as Adam

One major question for using 1-bit Adam is the convergence speed, and we find that 1-bit Adam can achieve the same convergence speed and comparable testing performance using the same number of training samples as shown in Figure 5.

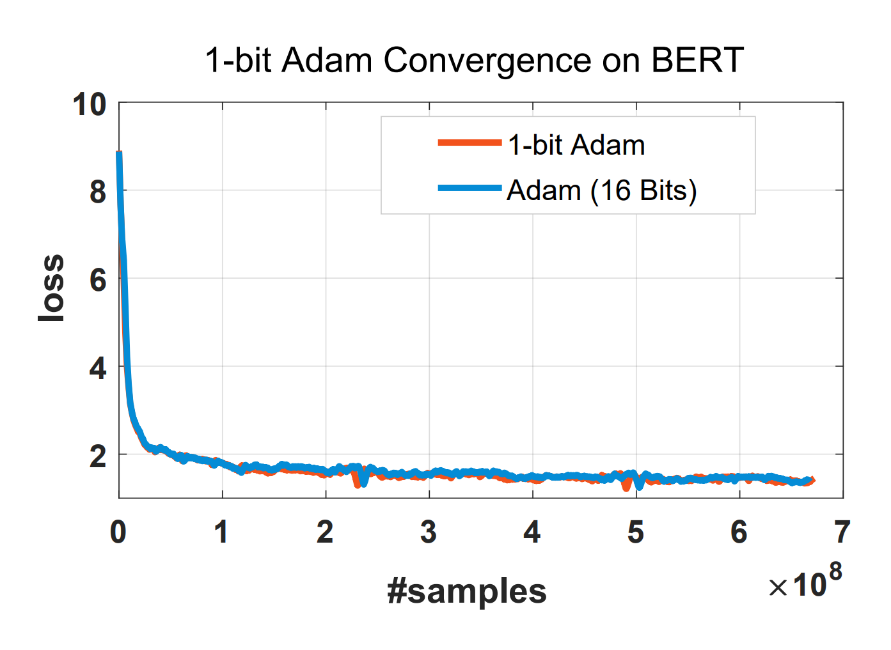
Figure 5: 1-bit Adam converges like Adam using the same number of training samples.

Detailed BERT-Base and BERT-Large results are shown in Table 1. We see that the scores are on par with or better than the original model for both the uncompressed and compressed cases.

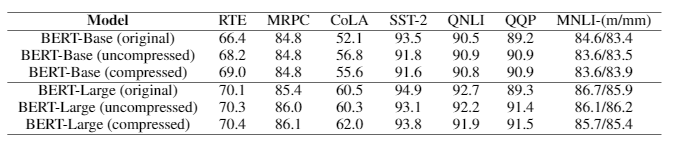
Table 1: Verifying correctness of 1-bit Adam on various testing tasks

Up to 5x less communication: 1-bit Adam provides the same convergence as Adam and reduces the communication volume by 16x during the compression stage for 16-bit (FP16) training. For BERT pretraining, this leads to an overall communication reduction of 5x as we observed the warmup stage to be just 15% of the end-to-end training time.

The formula to calculate the communication volume ratio of the original versus 1-bit Adam is as follows:

1 / (warmup + (1 – warmup)/16)

In the case of warmup equaling 15%, original Adam incurs 5x of the communication as 1-bit Adam.

1-bit Adam is 3.5x faster for training BERT-Large

We present two main results for training BERT-Large on systems with two different bandwidth-limited interconnects: 1) 40 gigabit Ethernet (Figure 5) and 2) 40 gbps InfiniBand QDR (Figure 6). During the compression phase, we observe up to 6.6x higher throughput on the system with Ethernet and up to 2x higher throughput on the system with InfiniBand, resulting in end-to-end speed up (including both warmup and compression stages) of 3.5x and 2.7x, respectively. The major benefit of 1-bit Adam comes from the communication volume reduction—enabled by our compressed momentum exchange—and from our custom allreduce operation that implements efficient 1-bit communication using non-blocking gather operations followed by an allgather operation.

It is important to note that one can also increase total batch size to reduce communication using optimizers like LAMB instead of Adam for BERT pretraining. However, 1-bit Adam avoids the need for rigorous hyperparameter tuning, which is often more difficult for large batches from our experience. Furthermore, 1-bit Adam also works very well for workloads that have small critical batch size (cannot converge well with large batch size) like many fine-tuning tasks.

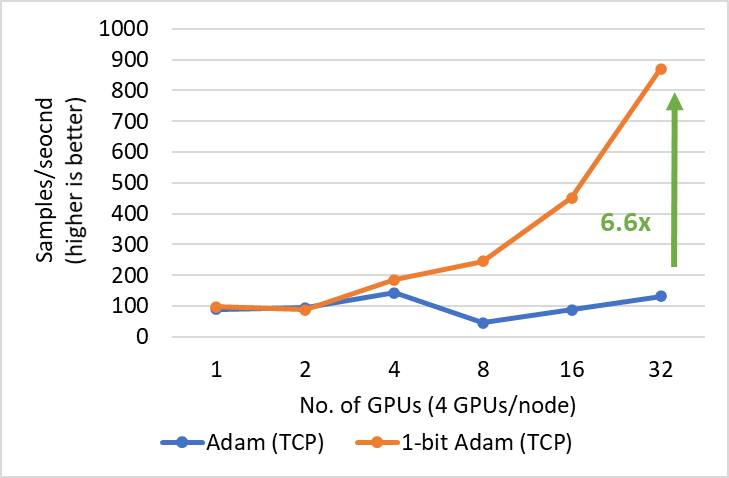
Figure 5: Performance of 1-bit Adam for BERT-Large training on 40 Gbps Ethernet interconnect during the compression stage.

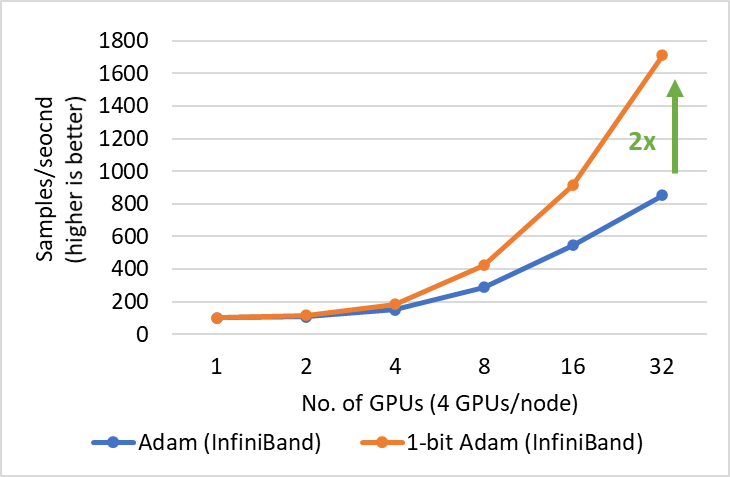
Figure 6: Performance of 1-bit Adam for BERT-Large training on 40 Gbps InfiniBand interconnect during the compression stage.

1-bit Adam is 2.7x faster for SQuAD fine-tuning

1-bit Adam offers scalability not only on large-scale training tasks but also on tasks like SQuAD fine-tuning. As shown in Figures 7 and 8, 1-bit Adam scales well on both Ethernet- and InfiniBand-based systems and offers up to 6.2x higher throughput (during the compression stage) on the Ethernet-based system, resulting in 2.7x end-to-end speedup (25% warmup plus 75% compression stage). For SQuAD fine-tuning, we observed that a total batch size of 96 offers the best F1 score. Batch sizes larger than this value lower the convergence rate and require additional hyperparameter tuning. Therefore, in order to scale to 32 GPUs, we can only apply a small batch size of 3-4 per GPU. This makes fine-tuning tasks communication intensive and hard to scale. 1-bit Adam addresses the scaling challenge well, obtaining 3.4x communication reduction without enlarging batch size, and it results in a 2.7x end-to-end speedup.

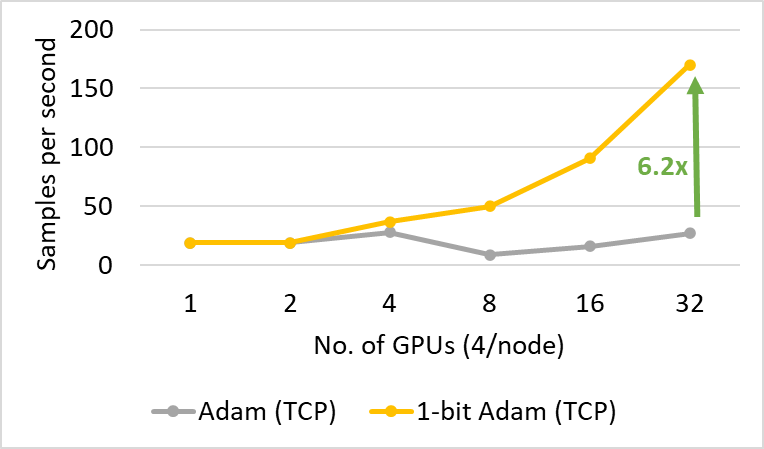
Figure 7: Performance of 1-bit Adam for SQuAD fine-tuning on 40 gbps Ethernet during the compression stage.

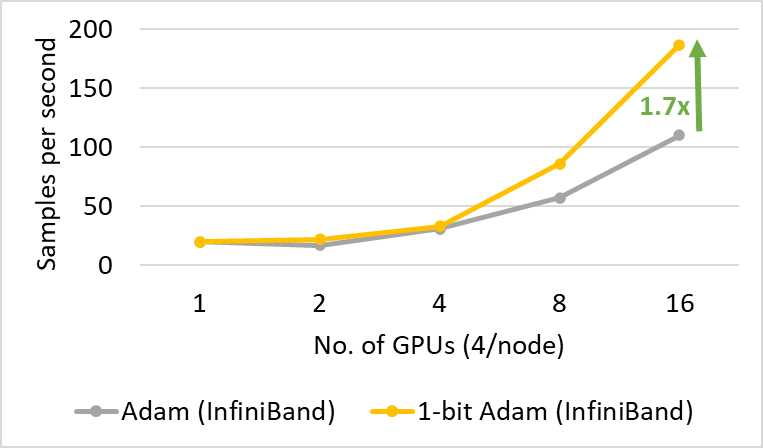
Figure 8: Performance of 1-bit Adam for SQuAD fine-tuning on 40 gbps InfiniBand interconnect during the compression stage.