Getting Started with DeepSpeed-MoE for Inferencing Large-Scale MoE Models
DeepSpeed-MoE Inference introduces several important features on top of the inference optimization for dense models (DeepSpeed-Inference blog post). It embraces several different types of parallelism, i.e. data-parallelism and tensor-slicing for the non-expert parameters and expert-parallelism and expert-slicing for the expert parameters. To maximize the aggregate memory-bandwidth, we provide the communication scheduling with parallelism coordination to effectively group and route tokens with the same critical-data-path. Moreover, we propose new modeling optimizations, PR-MoE and MoS, to reduce MoE model size while maintaining accuracy. For more information on the DeepSpeed MoE inference optimization, please refer to our blog post.
DeepSpeed provides a seamless inference mode for the variant of MoE models that are trained via the DeepSpeed-MoE library (MoE tutorial). To do so, one needs to simply use the deepspeed-inference engine to initialize the model to run the model in the eval mode.
MoE Inference Performance
In modern production environments, powerful DL models are often served using hundreds of GPU devices to meet the traffic demand and deliver low latency. It is important to explore how these two broad goals of high throughput and low latency can be realized for MoE model inference at scale.
For dense models, throughput can be increased by using multiple GPUs and data parallelism (independent replicas with no inter-GPU communication), whereas lower latency can be achieved by techniques like tensor-slicing to partition the model across multiple GPUs. The best case scaling in terms of total throughput is linear with respect to the increasing number of GPUs, i.e., a constant throughput per GPU. This is possible for pure data parallel inference scenarios as there is no communication between GPUs. To reduce latency, tensor-slicing style of model parallelism has proven to be beneficial but it comes with the cost - communication overhead between GPUs - which often lowers per GPU throughput and results in sublinear scaling of total throughput. In other words, for dense models, we cannot leverage parallelism to optimize both latency and throughput at the same time; there is a tradeoff between them. MoE inference, however, provides unique opportunities to offer optimized latency and throughput simultaneously while scaling to a large number of devices.
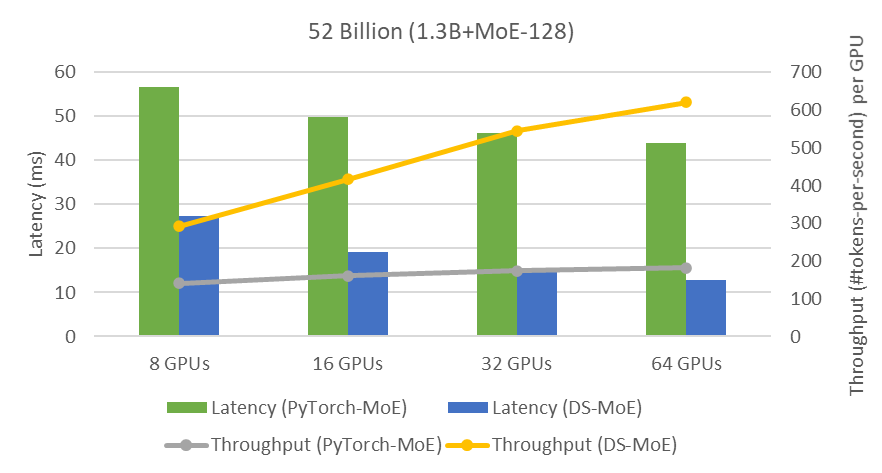
Figure below shows how we achieve both low latency and super-linear throughput increase simultaneously. We discuss this at length in our paper.
End-to-End MoE Inference Example
In this part, we elaborate the usage of MoE inference support in the DeepSpeed library using an end-to-end example.
Initializing for Inference
For inference with DeepSpeed-MoE, use init_inference API to load the DeepSpeed MoE model for inference. Here, you can specify the model-parallelism/tensor-slicing degree (mp_size), expert parallelism degree (ep_size), and number of experts (moe_experts). We create various process groups based on minimum of the world_size (total number of GPUs) and expert parallel size. By using this group, we can partition the experts among expert-parallel GPUs. If number of experts is lower than total number of GPUs, DeepSpeed-MoE leverages expert-slicing for partitioning the expert parameters between the expert-parallel GPUs. Furthermore, if the model has not been loaded with the appropriate checkpoint, you can also provide the checkpoint description using a json file or simply pass the 'checkpoint' path to load the model. To inject the high-performance inference kernels, you can set replace_with_kernel_inject to True.
import deepspeed
import torch.distributed as dist
# Set expert-parallel size
world_size = dist.get_world_size()
expert_parallel_size = min(world_size, args.num_experts)
# create the MoE model
moe_model = get_model(model, ep_size=expert_parallel_size)
...
# Initialize the DeepSpeed-Inference engine
ds_engine = deepspeed.init_inference(moe_model,
mp_size=tensor_slicing_size,
dtype=torch.half,
moe_experts=args.num_experts,
checkpoint=args.checkpoint_path,
replace_with_kernel_inject=True,)
model = ds_engine.module
output = model('Input String')
Various configuration options
Here, we show a text-generation example using an MoE model for which we can specify the model-parallel size and number of experts. DeepSpeed inference-engine takes care of creating the different parallelism groups using the tensor-slicing degree, number of experts, and the total number of GPUs used for running the MoE model. Regarding the expert parameters, we first use the expert-parallelism to assign each group of experts to one GPU. If number of GPUs is higher than number of experts, we use expert-slicing to partition each expert vertically/horizontally across the GPUs.
Let’s take a look at some of the parameters passed to run our example. Please refer to DeepSpeed-Example for a complete generate-text inference example.
generate_samples_gpt.py \
--tensor-model-parallel-size 1 \
--num-experts ${experts} \
--num-layers 24 \
--hidden-size 2048 \
--num-attention-heads 32 \
--max-position-embeddings 1024 \
--tokenizer-type GPT2BPETokenizer \
--load $checkpoint_path \
--fp16 \
--ds-inference \
Performance for standard MoE model
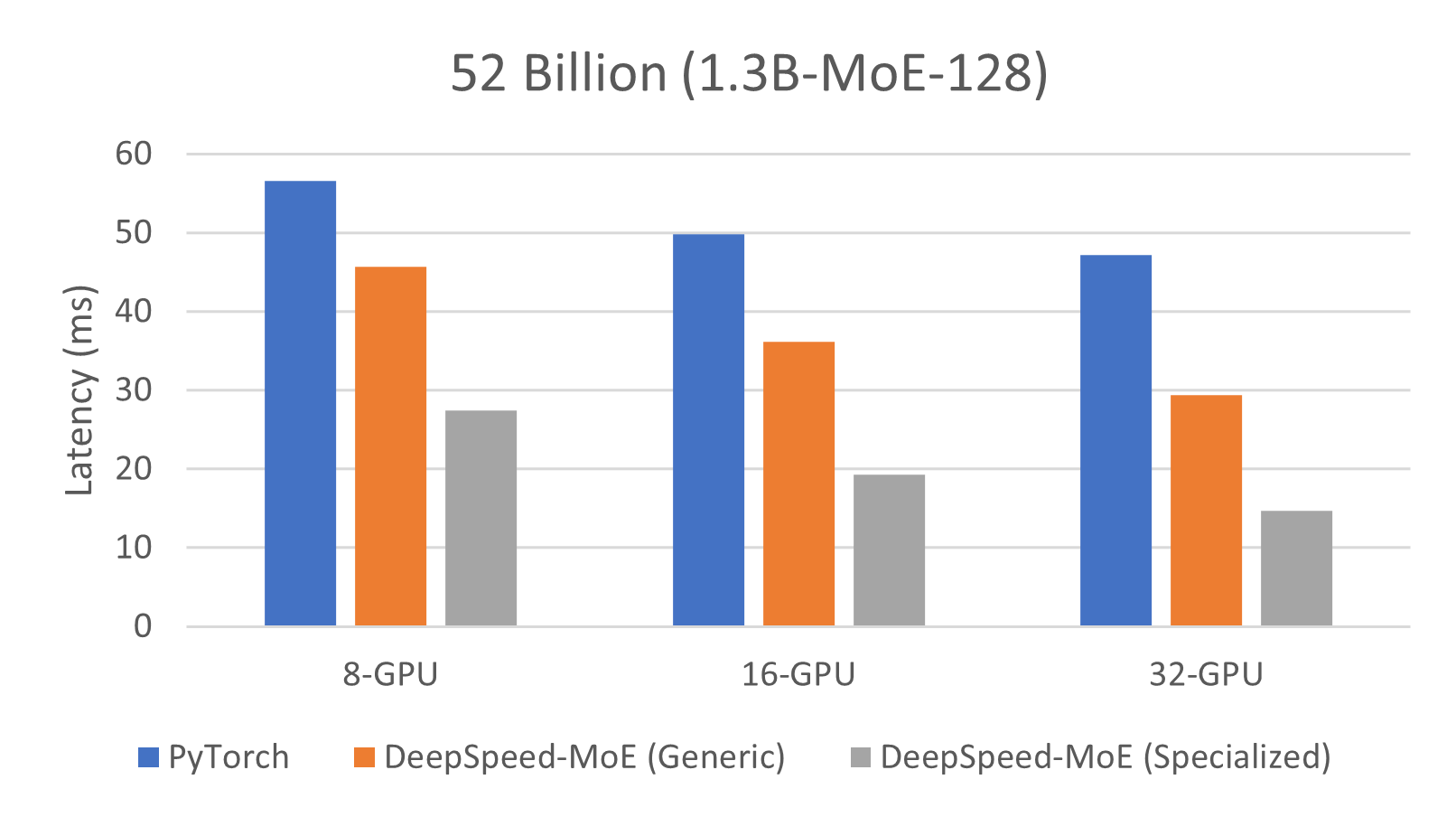
In order to show the performance scaling of DeepSpeed-MoE inference with increasing number of GPUs, we consider a 52B model architecture with 128 experts and 1.3B dense model using the parameters shown in the script above. In this example, we set tensor-slicing degree to one since the non-expert part of the model is relatively small (805M parameters). We use the last flag, ds-inference, to switch between DeepSpeed-MoE and PyTorch implementations.
For DeepSpeed-MoE inference, we show our results in this tutorial using two versions: 1) Generic, the current open source version of the DeepSpeed library that includes support for flexible parallelism and PR-MoE model optimization, and 2) Specialized, the most optimized version of DeepSpeed MoE inference system including special computation and communication kernels that will be released later. As mentioned in our blog post, MoE inference optimizations will be released in a staged fashion.
Figure below shows the inference performance of three different configuration, PyTorch, DeepSpeed-MoE (Generic), and DeepSpeed-MoE (Specialized), running on 8, 16, and 32 GPUs. Compared to PyTorch, DeepSpeed-MoE obtains significantly higher performance benefit as we increased the number of GPUs. By using the generic DeepSpeed-MoE inference, we can get between 24% to 60% performance improvement over PyTorch. Additionally, by enabling the full features of DeepSpeed-MoE inference, such as communication optimization and MoE customized kernels, the performance speedup gets boosted (2x – 3.2x).
Faster Performance and Lower Inference Cost using PR-MoE optimizations
To select between different MoE structures, we add a new parameter in our inference example, called mlp-type, to select between the 'standard' MoE structure and the 'residual' one to enable the modeling optimizations offered by PR-MoE. In addition to changing the mlp-type, we need to pass the number of experts differently when using PR-MoE. In contrast to standard MoE which uses the same number of experts for each MoE layer, PR-MoE uses different expert-count for the initial layers than the deeper layers of the network. Below is an example of PR-MoE using a mixture of 64 and 128 experts for every other layers:
experts="64 64 64 64 64 64 64 64 64 64 128 128"
generate_samples_gpt.py \
--tensor-model-parallel-size 1 \
--num-experts ${experts} \
--mlp_type 'residual' \
--num-layers 24 \
--hidden-size 2048 \
--num-attention-heads 16 \
--max-position-embeddings 1024 \
--tokenizer-type GPT2BPETokenizer \
--load $checkpoint_path \
--fp16 \
--ds-inference \
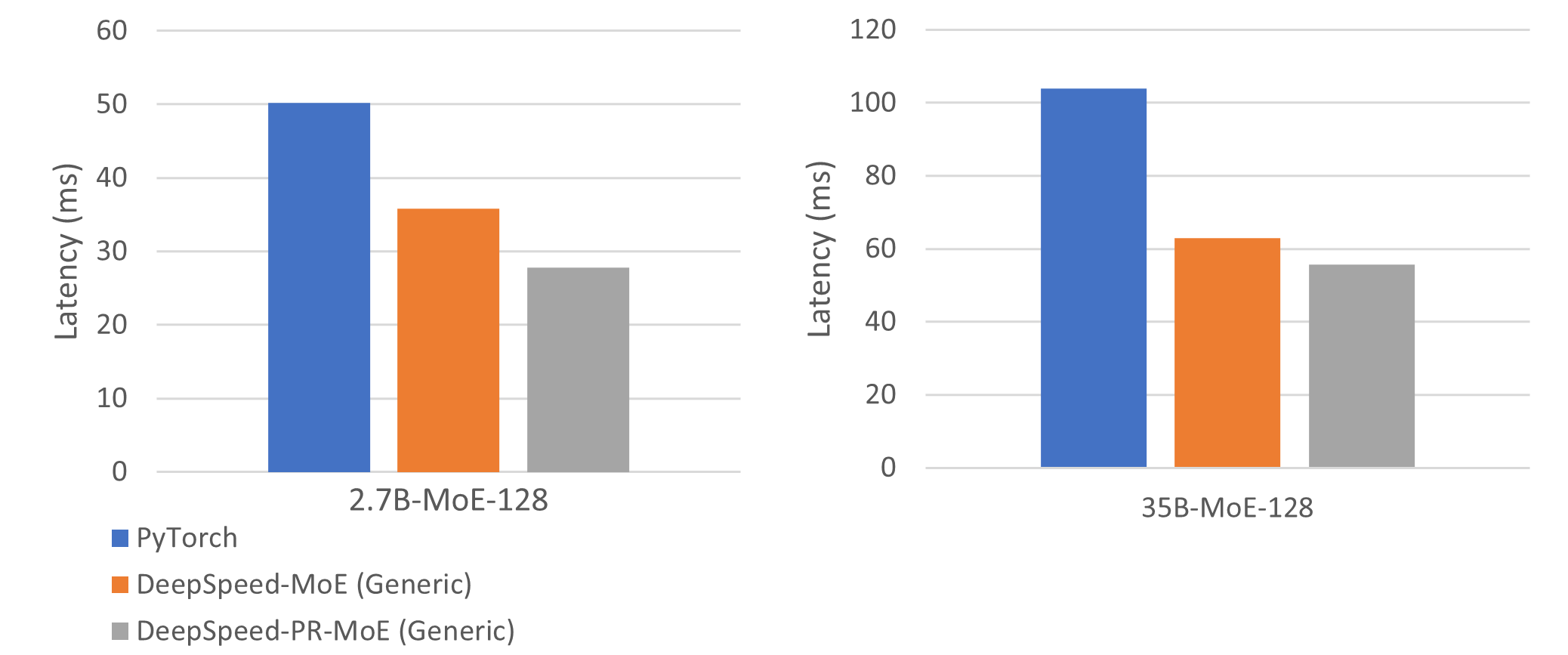
To evaluate the performance of PR-MoE, we use the two model structures, 'standard' and 'residual' and the configuration parameters as shown in the table below. Since we cannot fit the non-expert part of the 24B+MoE-128 on a single GPU, we use a model-parallel size larger than one. We choose the tensor-slicing degree in order to get the best performance benefit.
| Model | Size (billions) | #Layers | Hidden size | MP degree | EP degree |
|---|---|---|---|---|---|
| 2.4B+MoE-128 | 107.7 | 16 | 3584 | 1 | 64 - 128 |
| 24B+MoE-128 | 1046.9 | 30 | 8192 | 8 | 64 - 128 |
We use 1 node (8 A100 GPUs) to run inference on the 2.4B+MoE-128 and 8 nodes (64 A100 GPUs) for the 24B+MoE-128. Figure below shows the performance of three different configurations: MoE-Standard (PyTorch), MoE-Standard (DeepSpeed-Generic), PR-MoE (DeepSpeed-Generic). By using the standard-MoE DeepSpeed improves inference performance by 1.4x and 1.65x compared to PyTorch for the two models, respectively. Furthermore, by using the PR-MoE, we can improve the performance speedups to 1.81x and 1.87x, while keeping the model quality maintained.
More performance results and scaling toward bigger models and larger number of GPUs can be seen from our blog post and paper.
Congratulations! You have completed the DeepSpeed MoE inference tutorial.